高观点视角下的小学数学教学
发布时间:2018-09-13
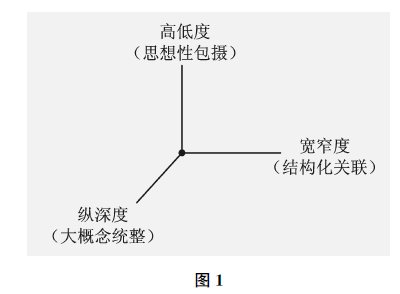
摘要:高观点的视角,可以处在数学的知识抽象性、概括性、包容性等相融合的高度,站在学科结构和学生认知结构相关联的宽度,立在知识性与思想性相统一的深度,使纵深度、宽窄度与高低度有机地构成知识呈现的三维空间结构,通过大概念统整、思想性包摄、结构化关联,促使小学数学教学呈现出新的景象与生机。
关键词:高观点小学数学大概念统整思想性包摄结构化关联
德国著名数学家、数学教育家克莱因倡导“高观点”,即从高等数学的角度来审视初等数学。的确,有许多初等数学的现象只有在非初等的理论结构内才能深刻地理解,这是高观点本初的内涵。但结合实际教学来看,高观点的内涵远不仅如此。高观点给初等数学的教学带来了生机与活力,藉此意蕴,我们认为,所谓“高”者,即不一般、优于常态也,高观点视角下的数学教学,也可以从内容的纵深维度迁移到内容的宽窄维度,推及思想的高低维度等等。
传统小学数学教学有着太多的疵议,存在许多不被重视的芥蒂。比如,“只见树木,不见森林”,教学中就题论题、就事论事,只看到单一的知识点而不及其余;比如,“只见皮囊,不见灵魂”,在重视知识、技能等知识“硬件”的同时,对隐含在知识内部的“软件”无知无觉,使数学教学呈现出“瘫”着的状态而“立”不起来;比如,“只重当下,不念过往”,表现在教学中就是“斩头去尾烧中段”,只对眼前的教学负责,对知识“从哪里来”“往何处去”不再关注也再不思考。
美丽的风景在远方,在深处,在高点。数学教学呼唤一种新的视角、新的境界,迫切需要一种新的教学理念来引领。而高观点的视角,可以处在数学的知识抽象性、概括性、包容性等相融合的高度,站在学科结构和学生认知结构相关联的宽度,立在知识性与思想性相统一的深度,使纵深度、宽窄度与高低度有机地构成知识呈现的三维空间结构(如图1),通过大概念统整、思想性包摄、结构化关联,促使小学数学教学呈现出一派新的景象与生机。
一、大概念统领
高观点视角下的小学数学教学首先体现为大概念统领。
大概念是美国教育心理学家奥苏伯尔所说的上位知识,它位于学科知识金字塔的顶端,其抽象性、概括性、包容性最高,解释力最强。借用生物学术语来说,大概念就是学科知识体系的内核,它内含遗传密码,最具再生力、生发力和预示力,是最具活性和繁殖性最强的一种知识类型,是其他知识得以生发与依附的主根。从学生学习的角度来看,大概念是一个纲,纲举目张;是一个组织者,整合所学的知识;是一根红线,把知识串起来。如果说学科知识体系具有一种“鹰架”式结构,那么,大概念就是撑起这一“鹰架”的支点,抓住了大概念,学科的其他知识和相应的学习活动就可以被提起来。可以说,大概念是学科整个学习活动的连心锁,是赋予学习活动整体性的关键。
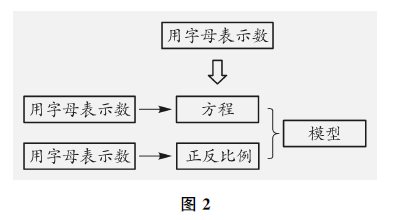
比如,“用字母表示数”就是一个大概念。它是代数学习的起始阶段和重要环节,理解用字母表示数的意义是运用代数式、方程、正反比例等进行交流的前提条件,是形成符号意识、代数思维的关键。它在整个知识体系中所处的位置可以用图2表示。
通过该内容的学习,经历由字母表示数、由日常语言表示数量关系到用符号语言表示数量关系的抽象过程,是学生数学思维发展的一次跨越,也是学生进一步学习代数知识乃至其他数学知识的基础。
再如,分数知识中的单位“1”也是一个大概念。教学“分数的意义”,很多教师对单位“1”的教学理解大多局限于教材,从文本出发,依次呈现“一个物体”“一个计量单位”“多个物体”三种素材中具体分数的含义,然后进行统整:“无论是一个物体、多个物体,还是一个计量单位,都有一个共同的名称,就叫单位‘1’,通常用自然数‘1’来表示。”这种“只见树木,不见森林”式的教学,导致学生对单位“1”的理解不具有多少生长性。我们不妨换一种视角。出示6个同样的小正方形,并引发思考:“这些小正方形该用什么数来表示呢?”学生展开想象,在充分的讨论、争辩中,形成“6个正方形可以用任何数来表示,关键看我们把多少个正方形看成‘1’,‘1’变了,这些正方形表示的数也就变了”的共识,从而理解了单位“1”的本质:整数就是单位“1”的叠加,有几个单位“1”,就可以用整数几来表示;如果不满1个单位“1”,或者比几个单位“1”还多一小部分时,就用分数来表示。这样的教学,单位“1”就跳出了一般性定义,而像一把“尺子”,成为一个被比的标准,在度量意义的视角下被赋予更深层的含义,充分体现了分数的最重要内涵,即它的无量纲性。
二、思想性包摄
高观点视角下的小学数学教学应该能看到知识深层的思想方法。
学科思想是学科知识中的“隐性内容”,是学科专家提出的对尔后学科发展和学科学习最具影响力的观念和见解,是知识“背后”的知识,是学科的精髓与灵魂。它是学科思维的“软件”,基于学科知识,又高于学科知识,与学科知识具有不可分割的辩证关系。因此,如何引导学生一起去找寻和发现学习中包蕴的数学思想、新的思维方法是数学教学所面临的挑战,因为如果内容选不准,不仅会浪费师生宝贵的学习资源,而且会错失和贻误学生智慧生长的“黄金期”。我们的数学教学,就是要帮助学生逐步建构起自己的“思想体系”“方法体系”,进而从不同的角度理解和认识问题,创造性地解决问题。
首先,从整体上构建教材中所蕴含的数学思想的立体框架。比如教学苏教版小学数学四年级下册“三位数乘两位数”,如果就事论事地进行浅表性分析,似乎很难看出其中的思想内核,但若能走进教材的深处,就能以数学思想为纽带串起整节课。在复习了“两位数乘两位数”的计算后,让学生直接尝试“三位数乘两位数”的算式并讲明道理,而后引发思考:“老师翻看了后面的教材,在四年级学完了三位数乘两位数之后,不再有四位数乘两位数或三位数乘三位数了,这是为什么呢?”通过思考让学生明白,所有多位数的乘法,都遵循着同一种运算思想,那就是“先分后合”,无论运算步数如何变化,但其中的思想原理是不变的。
其次,让数学思想有机融入数学知识的形成过程中。比如,人教版小学数学一年级上册第110页有这样的习题:
9+□<1518-□>1013+□<19
虽然这些题目只是要求学生在空格中填进一个合适的数,但我们应该明白,若把□换成x,则上面的题目就变成了不等式,这时x就是一个变元符号,就会有一定的取值范围,这一个“位置占有者”的作用就会凸显出来。教学时,我们可以引导学生思考、讨论:“□内最大能填几?最小呢?最多能填几个数?”同样,在此基础上还可进一步深化:“□+○<7,可以填些什么数?”这样的处理,更好地渗透了符号变元这一数学思想。
三、结构化关联
高观点视角的小学数学教学还应该能看到知识内在的结构。
学科之所以为学科,而不是简单概念与知识要点的堆砌,其中非常重要的原因就在于学科知识之间存在着不可割裂的内在联系。
所谓结构,简单地说,就是事物之间的联系,它表现为组织形式和构成秩序。从静态看,学科知识应该形成经纬交织、融会贯通的立体网络。从动态看,学科知识应该形成一个自我再生力强大的开放系统,以充分挖掘学科知识结构区别于科学知识结构的特有的功能。为此,我们必须合理设计教学,使前后知识内容互相蕴含、自然推演,编织一个具有生命力的、处于运动中的思维网络,引导学生深刻领会各个概念的实质,掌握蕴含在各个概念相互关系中的思维模式。
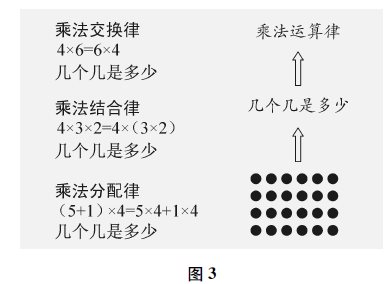
比如,乘法的三个运算律(乘法交换律、乘法结合律、乘法分配律)之间是有内在关联的,其本质是一致的,都是乘法意义的外在呈现。因此,教学“乘法分配律”时,有教师通过一张点子图(如图3)巧妙地将这三个运算律进行了统整:让学生根据“4×6=6×4”“4×3×2=4×(3×2)”“(5+1)×4=5×4+1×4”三道算式,在点子图上把各自的运算过程表示出来,然后通过对比发现:原来,无论是乘法交换律、乘法结合律还是乘法分配律,都求的是“几个几是多少”,都是根据乘法的意义衍生出来的。
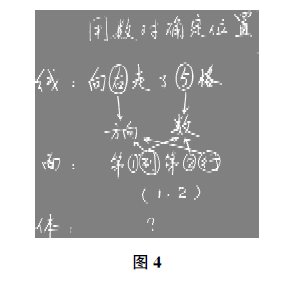
再如,“空间与图形”领域中“图形与位置”的相关内容主要包括:(1)二年级用“第几排第几个”等方式描述物体的位置;(2)五年级用“数对”表示方格图上点的位置;(3)六年级用“方向和距离”表示平面图上点的位置。这三部分内容虽然呈现出不同的教学层次,但内在的数学本质是一致的,即都与“方向”“距离”这两个要素密切相关。因而,教学“用数对确定位置”这一内容,我们不仅应该看到它的“今生”,还该看到它的“前世”与“后世”,即它“从哪里来”“将往哪里去”。为此,我创设了“小鸭在哪里”的情境,通过一维的“小鸭是怎么走的”的回忆,勾勒出全课的基调,即一个点的位置,既与方向有关,又跟“数”有关。在“数对”教学完毕后,再对知识的形成过程进行反溯,让学生感受到,数对也是方向与距离的衍生物,只不过在数量上由一个变成了两个(如图4)。在课的末尾,再通过“要是小鸭潜到了水底,该怎么确定它的位置呢”的追问,联结三维空间里点的位置的确定,引导学生大胆想象,并在学生处于朦朦胧胧的感觉之时,让教学“戛然而止”。
此时,在学生的认知结构中若隐若现留下的,是知识的全貌,是结构的雏形,更是朝向未来知识世界的美好。